一般化された嘘理論と応用のジャーナル

Let 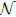be the Lie algebra of all n × n strictly block upper triangular matrices over a field 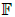. In this paper, we explicitly describe all Lie triple derivations of 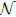when char(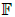)≠2.

Using Jiang function we prove the fundamental theorem in arithmetic progression of primes. The primes contain only k<P_g+1 long arithmetic progression, but the primes have no k>P_g+1 long arithmetic progressions theorem.

The purpose of the article is to describe all 3-dimensional subalgebras and all corresponding reductive pairs of Lie algebra of all 2 × 2 real matrices. This Lie algebra is 4-dimensional as a vector space, it’s not simple, and it’s not solvable. The evaluation procedure utilizes the canonical bases for subspaces that were introduced. In Part I of this article, all 3-dimensional subalgebras of the given Lie algebra g are classified. All reductive pairs {h, m} with 3-dimensional subalgebras h are found in Part II. Surprisingly, there is only one reductive pair {h, m} with special 3-dimensional subalgebra h and 1-dimensional complement m. Finally, all reductive pairs {h, m} with 1-dimensional subalgebras h of algebra g are classified in Part III of the article.

Here we provide the step by step procedure to end that the Generalized Lie Theory converges to one solution, that is the Universe. We consider the Hyperbola; Rotation Matrix, the Cross and Dot Products; Euler’s formula, Communicator, and Astrotheology Mathematics. They all converge to one final solution.

The Universal Parametric EquationIn this paper, we use Astrotheology (AT) Mathematics and linear algebra to develop a Universal Parametric Equation. We consider Energy, Gravity, Green’s Theorem the Clairnaut D.E., Matrices and Euler’s identity to derive a plot of the parametric equation which has critical values where it crosses itself or becomes a point.

The purpose of the article is to describe all 2-dimensional subalgebras and all corresponding reductive pairs of Lie algebra g of all 2 × 2 real matrices. This Lie algebra is 4-dimensional as a vector space, it’s not simple, and it’s not solvable. The evaluation procedure utilizes canonical bases for subspaces that were introduced. Part I of the article contains necessary basic information. In Part II, all 2-dimensional subalgebras of the given Lie algebra g are classified. All reductive pairs { , m} with 2-dimensional subalgebras h are found in Part III. The separate article contributes classification of all 3-dimensional subalgebras and its reductive pairs. Together, both articles give the total classification of all subalgebras and all reductive pairs of Lie algebra g.

BiHom-Lie algebra is a generalized Hom-Lie algebra endowed with two commuting multiplicative linear maps. This paper is devoted to investigate the generalized derivation of BiHom-Lie algebra. We generalize the main results of Leger and Luks to the case of BiHom-Lie algebra. Firstly we review some concepts associated with BiHom-Lie algebra L. Furthermore, we give the definitions of the generalized derivation GDer(L), quasiderivations QDer(L), center derivation Z(L), centroid C(L) and quasicentroid QC(L). Later one, we give some useful proprieties and connections between these derivations. In particular, we prove that GDer(L)=QDer(L)+QC(L). We also prove that QDer(L) can be embedded as derivations in larger BiHom-Lie algebra.

Definition of theorem: On a politic map, the neighbour countries can not to take the same colour because they could seem the same country. When the frontier between countries is a point, we must not consider it as a frontier. This is possible with three and five colours, it is proved, but with four at this moment lack an evident proof, without pc. There are infinite maps where the solution must to run, also inside of them it must to solve the relation between infinite and only four colours. For that I transform politic maps into maps in the plane graph, then I use their polygons to create other new polygons, with a particular centre. Then the group of new polygons form a structure, which distribute all points in two independent substructures, the Centres and the Crowns. This particular centre is the common vertex of some polygons belonging to plane graph, and they form a new polygon. The points which surround the centre constitute a barrier that impede the direct relation between the centre and other points. I call crown to this barrier. Each polygon is linked with the previous, so it achieves shape of spiral. Also it achieves independence among centres, and the points of the same crown do not entwine, their relations are consecutives, two by two. To specify the new structure group points in two substructures, the Centres and the Crowns, one colour goes to the centres, and three to the crowns. On the crown there is a process of colours run on a finite number of points chosen by triangulations, which impose a Stopping Condition. The triangulation happens when two or more points with two different colours have a common neighbour, then this point must to take the third colour. On each process after last triangulation happen always stopping condition, it mean that neighbour points without colours have two possibilities, and the rest three, which guarantee the resolution. The global outcome is a Big Crown biggest after each process, whose internal points and their links do not influence on the following points. There are two graphics files, Formation of structure and Plans, where I change the three colours by three shapes: triangle, circle and square. I recommend to see the two graphics files consecutively

In this paper, I attempt to answer the philosophical problem of is the Universe Continuous or Discrete. The answer is that it both ant the same time. It is the tension between these that create the phenomena that the human mind perceives as reality. The method used to decipher this perplexing and complex problem is solved by using Astrotheology Mathematics. It has wider implications in the very nature of God and light.

We completely resolve the boundary value problem for differential forms for conformal Einstein infinity in terms of the dual Hahn polynomials. Consequently, we present explicit formulas for the Branson-Gover operators on Einstein manifolds and prove their representation as a product of second order operators. This leads to an explicit description of Q-curvature and gauge companion operators on differential forms.

We have general frameworks to obtain Poincare polynomials for Finite and also Affine types of Kac-Moody Lie algebras. Very little is known however beyond Affine ones, though we have a constructive theorem which can be applied both for finite and infinite cases. One can conclusively said that theorem gives the Poincare polynomial P(G) of a Kac-Moody Lie algebra G in the product form P(G)=P(g) R where g is a precisely chosen sub-algebra of G and R is a rational function. Not in the way which theorem says but, at least for 48 hyperbolic Lie algebras considered in this work, we have shown that there is another way of choosing a sub-algebra in such a way that R appears to be the inverse of a finite polynomial. It is clear that a rational function or its inverse can not be expressed in the form of a finite polynomial.

Our method is based on numerical calculations and results are given for each and every one of 48 Hyperbolic Lie algebras.

In an illustrative example however, we will give how above-mentioned theorem gives us rational functions in which case we find a finite polynomial for which theorem fails to obtain.

We propose a new method to calculate coupling coefficients of E7 tensor products. Our method is based on explicit use of E7 characters in the definition of a tensor product. When applying Weyl character formula for E7 Lie algebra, one needs to make sums over 2903040 elements of E7 Weyl group. To implement such enormous sums, we show we have a way which makes their calculations possible. This will be accomplished by decomposing an E7 character into 72 participating A7 characters.

Notes for some talks given at the seminar on characteristic classes at NTNU in autumn 2006. In the note a proof of the existence of a Chern-character from complex K-theory to any cohomology Lie theory with values in graded Q-algebras equipped with a theory of characteristic classes is given. It respects the Adams and Steenrod operations.

In this paper, we define invariant tensor product and study invariant tensor products associated with discrete series representations. Let G(V₁)×G(V₂) be a pair of classical groups diagonally embedded in G(V₁⊕V₂). Suppose that dimV₁<dimV₂. Let π be a discrete series representation of G(V₁⊕V₂). We prove that the functor π ⊗_G(V1) *maps unitary representations of G(V₁) to unitary representations of G(V₂). Here we enlarge the definition of unitary representations by including the zero dimensional representation.

As it is well known, the Lie theory is solely applicable to dynamical systems consisting of point-like particles moving in vacuum under linear and Hamiltonian interactions (systems known as exterior dynamical systems). One of the authors (R.M. Santilli) has proposed an axiom-preserving broadening of the Lie theory, known as the Lie-Santilli isotheory, that is applicable to dynamical; systems of extended, non-spherical and deformable particles moving within a physical medium under Hamiltonian as well as non-linear and non-Hamiltonian interactions (broader systems known as interior dynamical systems). In this paper, we study apparently for the first time regular and irregular isorepresentations of Lie-Santilli isoalgebras occurring when the structure quantities are constants or functions, respectively. A number of applications to particle and nuclear physics are indicated. It should be indicated that this paper is specifically devoted to the study of isorepresentations under the assumption of a knowledge of the Lie-Santilli isotheory, as well as of the isotopies of the various branches of 20th century applied mathematics, collectively known as isomathematics, which is crucial for the consistent formulation and elaboration of isotheories.